Chapter 10.1 Parbolas
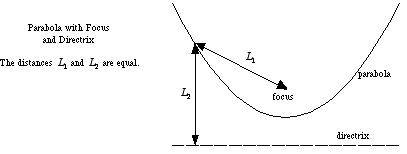
Parabola- set of all points equidistant from a fixed line (directrix) and a fixed point (focus)
Directrix- A line perpendicular to the axis of symmetry
Focus- A point that is the same distance from the vertex of a porabola as the directrix
Standard form of a parabola with vertex (h,k)
a fixed line (directrix) and a fixed point (focus)
1. (x-h)2 = 4p (y-k) [If the parabola opens up/down]
2. (y-k)2 = 4p (x-h) [If the parabola opens right/left]
(P is the distance between from vertex to the focus/directrix.)
If the value of 4p is positive, the parabola will open up or to the right

If the value of 4p is negative, the parabola will open down or to the left
Graphing a Parabola
To graph a parabola, use the standard from of the equation: ex. %5E2) =(y+2)
=(y+2)
Pull out the vertex (h,k)
so in the example, the vertex of the parabola is (1,-2)
change the sighns of the X and Y values when you take them from the equation
Next, pull out the value of 4p.
The value before the (y+2) equation in this example is equivalent to 4p.
So 4p=1.
Solve for p 1/4=0.25 (so p= 0.25)
Now, Take the value of p and find the location of the directrix and the focus.
Take the vertex of the elipse (1,-2) and add the value of p to the x or y
value depending on which direction your parabola opens and which
variable is the squared quantity.
In the example, x is the squared quantity and the value of 4p
is positive so the parabola will open upwards.
So, take the value of p and add it to the y value to find the focus.
[(1, -2+0.25) = (1, -1.75) is the focus.]
Then, subtract the value of p from the y coordinate of the vertex.
[-2-0.25= -2.25]
The directrix of the example is y= -2.25.
Ex) Find vertex, focus, directrix, and AOS
(Axis of Symetry) for )
1) First step is to move the constant (move to the side without the square)

2) Second step is to complete the square


3) Factor both sides
%3D%20(x%2B1)%5E2)
|
Vertex (-1,1)
|
| p=-1/2 |
| Focus= (-1,1/2) |
| Directrix y=3/2 |
| AOS x=-1 |
Take a look at this movie it walks you step by step throught the process:
http://www.youtube.com/watch?v=b7zXeVUz_r0
Still need help with parabolas? check out some of these places for help:
http://tutorial.math.lamar.edu/Classes/Alg/Parabolas.aspx
http://hyper-ad.com/tutoring/math/algebra/Quadratic_theory.html
Or here is a cool online place to graph parabolas:
http://www.coolmath.com/graphit/
Comments (0)
You don't have permission to comment on this page.