Rational Functions and Asymptotes
Rational function notation is f(x)= N(x)/D(x)!!!! A rational function is formed when a polynomial is divided by another polynomial.

An asymptote is a line that a graph approaches
and HARDLY ever crosses.
Check out this cool asymptote!
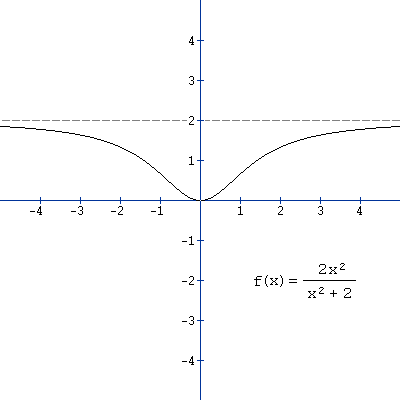
To find a verticle asymptote, set the the denominator=0
( A graph will NEVER cross a vertical asymptote!)
Ex: f(x)= 2x^2+11
x^2+x-20
vertical asymptotes: x=-5 x=4
f(x)= 2x^2+11
(x+5)(x-4)
x+5=0 x-4=0
x=-5 x=4
To find a horizontal asymptote, compare the degrees of the numerator and denominator.
IF...
The numerator is less than the denominator then the horizontal asymptote is y=0 ex. 4x^2+3h.a y=0
3x^3+5
The numerator is greater than the denominator there is no horizontal asymptote ex. 2x^3+5 h.a none
x^2+x+20
The numerator is equal to the denominator the horizontal asymptote= the coefficient of numerator degree
the coefficient of denominator degree
ex. 2x^2+7 h.a y= 2
5x^2+3 5
Finding the Domain is easy!
Domain: The domain of a function is the set of all possible input values (usually x), which allows the function formula to work.
1. Find vertical asymptotes
2. Give all possible x's in parenthetic notation and exclude the vertical asymptotes
Ex. f(x)= 2x^2+3 f(x)= 2x^2+3 vertical asymp. x=-5 x=4
x^2+x-20 (x+5)(x-4)
DOMAIN: (-¥ ,-5)U(-5,4)U(4,¥ )
To learn more about Rational Functions and Asymptotes visit this very informative website: http://people.richland.edu/james/lecture/m116/polynomials/rational.html
Here is a video to help you better understand solving and graphing asymptotes

Comments (0)
You don't have permission to comment on this page.