2.3 Real Zeros of Polynomial Functions
Polynomial Function: F(x)= 
To find real zeros of polynomial functions you can:
1. Divide by known factors (synthetic division/quadratic formula)
- If x-a is a factor, factor it out of the equation by using synthetic division
- If the remainder is zero, then the number is a factor
Example #1:
Is x- a factor of
a factor of  -2x+3
-2x+3
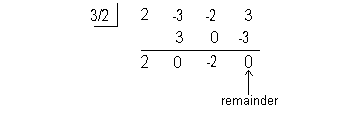
Yes, x- is a factor of
is a factor of  -2x+3
-2x+3
- after factoring out x- , keep factoring until simplified
, keep factoring until simplified
- solve the problem to find the zeros
Link to see more examples:
http://id.mind.net/~zona/mmts/functionInstitute/polynomialFunctions/roots/syntheticDivision.html
2. Rational Root Therom
Rational Root Therom: All possible rational roots are of the for  .
.
p-- factors of last tern of the polynomial function
q-- factors of the first term of the polynomial function
Example #2:
Find all possible rational roots in the equation F(x)=
1 + 12
+ 12
p--  1, 2, 3, 4, 6, 12
1, 2, 3, 4, 6, 12
q--  1
1

= –12, –6, –4, –3, –2, –1, 1, 2, 3, 4, 6, 12
For further explination visit http://www.purplemath.com/modules/rtnlroot2.htm
3. Graph
- Plug in the equation to the calculator
Example #3: Graph f(x)= 

x = -2, 1, 3
-zeros cross the x-axis
-to find zeros using calculator second trace (calc) zero
Example #4: Graph f(x)= 

x= -1, 2
Now it's your turn!
Is (x-1) a factor of the following?
1. f(x) = x4 - 2x3 + x - 2
2. f(x) = x3 + 2x2 - 3x + 1
Use the Rational Root Therom to find out the rational roots.
1. f(x) = x4 - 2x3 + x - 2
2. f(x) = x3 + 2x2 - 3x + 1
Graph the polynomial functions.
1. f(x) = x4 - 2x3 + x - 2
2. f(x) = x3 + 2x2 - 3x + 1
Link to the polynomial function zero video:
http://videos.howstuffworks.com/hsw/11298-polynomial-functions-the-zero-property-video.htm
Comments (0)
You don't have permission to comment on this page.